Space Infantry’s Registered Nurse

If we ignore 2020 (and I've yet to hear a compelling reason not to do so), then this new post isn't really that delayed.

Space Infantry: Resurgence takes much from the original Space Infantry: the high difficulty; the great narrative; the simple-but-effective core system; all the ambiguities, typos, and errata. But one thing it left behind, thankfully, was the chit-pull system.

The designer notes discuss the issue in regards to the lack of replacement, but my main beef with the chits was simply that it took too long and slowed down an otherwise smooth system. Pulls from a bag have their place and can be very effectively used. But in my experience with the original, nothing much was gained but friction.

In Resurgence, a roll of a d6 can be used. Quick and easy.

However, the player is given the option to use a slightly more complicated system to produce a number between 0 and 8. And it works like so:

You roll a d6. If you get a 1, you roll another d6 and if it's a 1 or 2, then your final result is a 0, otherwise it stays a 1. If your original roll is 2-5, then your final result is whatever you rolled. If your original roll is a 6, then you roll another d6; if you get a 1 then your final result is a 7, if you get a 2 then your final result is an 8, and if you get a 3 or higher then your final result is a 6.

It sounds WAY more complicated written that way than it actually is.

My aim is to look at the difference in the distribution of these two systems and how they effect common situations in the game.

(Note: I'm just using the basic stuff here. I am not factoring in items or experience or anything like that. Nor am I doing any joint probabilities from using command points to increase AP [not like my squad leader ever produces any CP anyway, AMIRIGHT?])

First, probabilities.

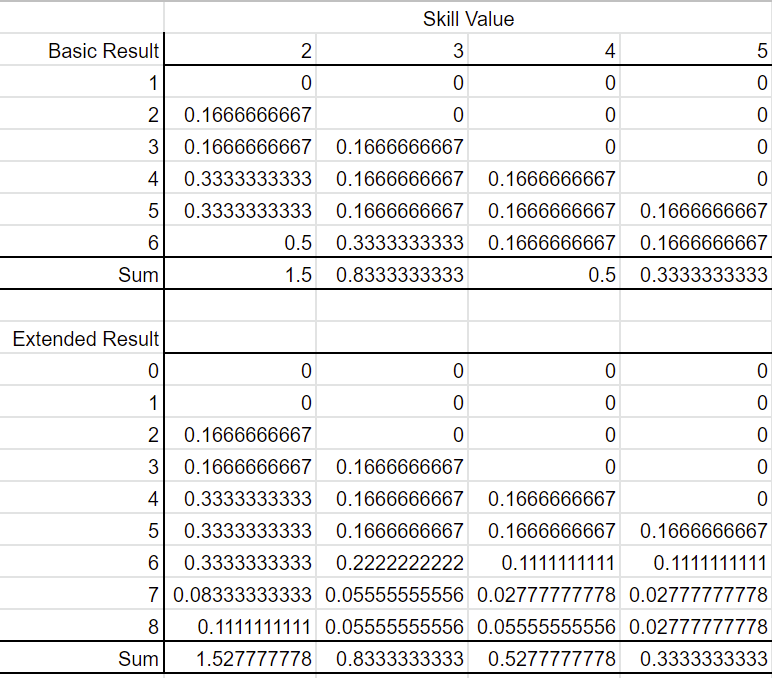
On a regular ol' d6 you've got a 1/6 chance of any particular number coming up. So each value is equally likely, each with a 16.67% chance of showing up.

In the extended system, however, you've got to factor in the results of both dice. Since the results of each die are independent, you can multiply them together to get the probability of them occurring concurrently.

So for a 0, you have to roll a 1 on the first die and a 1 or 2 on the second die. This is a (1/6)*(2/6) chance, or 2/36, or 1/18, or 5.56%.

For a 1, you have to roll a 1 on the first die and NOT roll a 1 or 2 on the second die. This is a (1/6)*(4/6) chance, or 4/36, or 1/9, or 11.12%.

(Note that these are mutually exclusive events [they can't both happen], so you can sum them to get the probability that one or the other of them happens. Which is the same as saying you get a 1 on the first die and any roll on the second die. The sum of these is 6/36 or 16.67%: the probability of rolling a 1.)

For a 2, 3, 4, or 5 there's no change. So each of those is a 16.67% chance like normal.

For a 6, you have to roll a 6 on the first die and then NOT roll a 1 or a 2 on the second. This is the same probability as getting a 1, 11.12%.

For a 7, you have to roll a 6 on the first die and a 1 on the second die. That is a (1/6)*(1/6) chance, or 1/36, or 2.78%.

For an 8, you have to roll a 6 on the first die and a 2 on the second die. That's the same probability as a 7, so it's 2.78%.

These all sum up to 100%, meaning that, luckily, in Space Infantry: Resurgence, if you roll the dice you WILL, in fact, get some sort of result.

How about pictures?

This is all well and good, but what does it mean for the GAME? Well, let's start with seeing if it changes the expected value of your roll.

The expected value is sort of an average of what you'd expect to get if you rolled infinitely. It's the theoretical mean of the distribution of your dice. You get it by multiplying your result by the probability of that result, and adding those all up.

So for a regular d6 you'd have this:

[1*(1/6)] + [2*(1/6)] + [3*(1/6)] + [4*(1/6)] + [5*(1/6)] + [6*(1/6)]

= 3.5. So your mean result on a regular d6 is 3.5.

For the extended die roll, though, you have:

[0*(1/18)] + [1*(1/9)] + [2*(1/6)] + [3*(1/6)] + [4*(1/6)] + [5*(1/6)] + [6*(1/9)] + [7*(1/36)] + [8*(1/36)]

= 3.5278

Ever so slightly higher. So technically using the extended dice system over many rolls will result in die rolls averaging higher than the basic system. By less than a 1% increase (0.794%).

This is really only one part of the story, though. Yes, your rolls may be slightly higher on average, but what does it mean for the game?

In clinical trials there's the concept of "clinically meaningful." When testing a drug, you might be able to show that some measured result is different for people on the drug than people taking placebo. And though you do want the result to be statistically different, you also need it to be clinically meaningful. If the change in the value of that result doesn't actually make the subject feel any better, then what's the point?

So yes, there is a slight advantage numerically to using the extended dice, but is it clinically meaningful? That's a call based on what effect it actually has on the game. Is it going to make you feel better?

Let's look at a few common die resolutions (in the base non-campaign game, for now) and see what difference this would make.

By far what I care most about is test resolution. If I use this, what changes in terms of command points generated, wounds generated, wounds received, etc.

For the uninitiated: friendly and enemy units in SI and SI:R all have values they use for node resolution (getting around) and combat. You roll the dice and divide what you get by the unit's value in whatever you're testing. Ignoring any remainder, the result is how many success levels you get.

So if your skill is 3 and you roll (using basic) a 1 or 2 you generate no successes. If you roll a 3, 4, or 5 you generate one success. If you roll a 6 you generate two successes. So lower numbers on skills are better, and higher rolls are better.

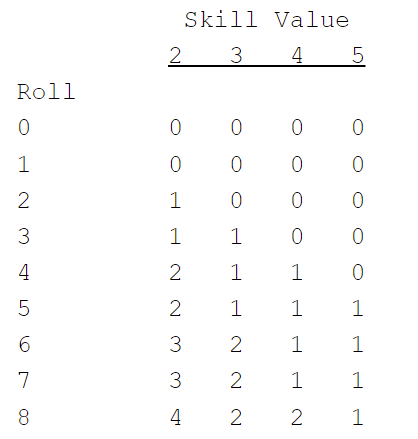
So let's see the options. Here's how many successes you get for each possible roll based on your skill value:

One of the shifting probabilities between the basic and extended versions is that it is impossible to roll a 0, 7, or 8 using the basic version.

Does the 0 change anything? With skill values 2-5, not really. If you roll a 1 on the first roll, you're not generating any successes no matter how you swing it, and the probabilities are same (basic 1 is the same as extended 0 or 1). Now, there are instances where it might matter. If you had someone with 1 skill, then you do care about the difference between a 0 and a 1. And someone with a skill of 2 could use a command point to still generate a success on a roll of a 1, so the basic's a bit better for them. Outside of those edge cases, it's not hugely different.

At the top end, things do change a bit more. Rolling an 8 is the only way a character with skill 4 (pretty common) can generate two successes. Specifically, your squad leader starts with a command skill of 4, and it sure is great to at least have a CHANCE that they'll make two command points.

So our slightly higher expected value of our rolls only really matters if it translates into a higher expected value of successes. So again, we'll multiply the number of successes by the probability you generate that number, then add 'em all up.

So what are we looking at?

Each column are the skill values 2 to 5. Down the left are your possible rolls, the top set using the basic system and the bottom set using the extended mechanic. Each cell is the probability of rolling that result multiplied by the number of success you'd get for that result at that skill level. The sum at the bottom of each section, then, is the expected number of successes you will get for a roll at that skill level.

Let's discuss it by looking at skill 4, as that's a skill you'll roll against often, especially to get command points in the base game.

Using the basic rolls, you'll get no success on a 1, 2, or 3. And you'll get 1 success on a 4, 5, or 6. So on average, you'll get a half a success.

Using the extended rolling mechanic, however, things are slightly different. You get nothing on a 1, 2, or 3 still. And you get nothing on a 0, either, but that won't affect the comparison to the basic system because you can only get a 0 if you start by rolling a 1 and you don't get anything on a 1 anyway.

Where things change is up top. Using the extended rolls, if you roll a 4, 5, or 6 on the first roll you will generate at least one success. The difference is that 1/6th of the time that you roll a 6, you'll generate TWO successes. And that 1/36th chance of one more success puts your expected successes at slightly higher than the basic version (a 5.56% increase). You get none of the negatives (a 1 is a fail no matter if it turns into a 0 or not) but there's a small chance of a bonus.

(By the way, all of this ultimately due to the fact that the distribution is unbalanced, as you can see in the red and blue graph. The probability of a 0 is the same as the probability of a 7 OR an 8. But an 8 is better. So the places in the game where that makes a difference [like 1, 2, or 4 skill] get a benefit. If your six just turned into a 7 on a second roll of a 1 or 2, this would mostly not matter.)

Let's look at 5 skill. Looking two charts up, you're only ever going to make 0 or 1 success with 5 skill. If you get a 5 or higher, you get a success. And that happens a third of the time, so your expected value is 0.3333.

Thing is, using extended (and similar to the 4 skill test), a 1 is a failure whether it flips to a 0 or not. But unlike 4 skill, a 6 is one success whether it improves to a 7 or 8 or not. It's still a 1/3 chance that you roll a 5 or higher, it's just the extended version spreads those probabilities over more numbers. With no way to roll a 10, you're still stuck at an expected success value of 0.3333. Same thing happens for 3 skill, since you can't roll a 9. For these skill levels, the chance for higher roll totals is not clinically meaningful.

For skill values >1, a result of a 1 on the first die rolled is a fail no matter the version you're using. And since higher rolls are better, you will always do at least as well, if not better, using the extended rolls.

For a skill value of 1, the expected value of success is the same as the expected value of the die roll (since a skill value of one means you generate successes equal to the value rolled). So in this one instance a roll on the first die of a 1 is not the same across both versions of the rolling mechanic, but the 1/3 chance that that one becomes a zero is outweighed by the 1/6 chance you get 7 successes and the 1/6 chance you get 8. From above, the EVs are 3.5 for basic, and 3.5278 for extended.

So, yes, at least for skill tests, the extended version is going to give you SLIGHTLY better results in the long run. However, the extended version is going to apply to enemies as well, so Beast Masters coming at you with 4 melee skill are going to do slightly more hurt to you as well.

What about other rolls?

Unskilled node resolution gives you a success on a 6 or higher. Since, in the extended, you will always get a 6 or higher if you roll a 6 on the first roll, there's no difference in probabilities here. You've got a 1/6 chance of a six in basic, and a (4/36)+(1/36)+(1/36) = 1/6 chance of a 6 or higher on extended. Might as well toss one die.

Same goes for armor rolls. A 4+ is the same no matter which version you use. I'm not scanning through the cards, but since the event strings are designed to work with either system, I would also guess that none of them are affected either. Like the skill tests, unless the results will change on the roll of a 0, 7, or 8, it's not going matter. Flame damage and poison would be similarly unaffected.

When you hoof it back to an explored node you buy a free turn if you roll a 6 or higher. So like the above, this is no different in either system. However, if you roll a 0 you have an event, and this can only happen in the extended version. So for travelling to explored nodes, the extended version is strictly worse for the player. 5.56% of the time you'll be taking on another A event. Does this make up for the slightly higher success average?

There are other rolls in the game, but most of them are harder to quantify.

For example, enemy unit selection has options for rolls of 0, 7, and 8. But the outcomes are different unit mixes that can't be easily quantified, so the comparisons are tough. A 7+ is as likely as a 0, so you'd have to look at the enemy units spawned at those values and see if adding the risk of a 7+ is worth the equal chance of rolling a 0.

So where does that leave us?

For many rolls, it won't matter. For skill tests, the extended increases successes, but that applies to the enemies as much as it does your infantry. And then there's the added chance of that critical failure and a group of baddies showing up in a previously explored node. Overall, as far as the math, it sorta seems like a wash? Maybe?

Except for one thing, and the reason I still recommend using it.

It's fun! This is a game, after all.

We've been looking at expected values, which by definition smooths over the highs and lows a bit. But we haven't looked at the variability of the possible values between these two systems.

No one remembers their average number of successes over the course of the game. That's not what we're here for. That's not what makes you pump a fist or break your pencil in half. That's not what session reports are made of.

They're made of that one turn, when, on the brink of death, you roll that 8 for your grenade and your one surviving assault team limps out of the last room covered in a red mist. They're made of that game where, levelled up and cocksure, you roll zero after zero in explored nodes and succumb to the biggest swarm you've ever seen. They're made from unforeseen circumstances, critical failures, Hail Marys, bad calls, and hero moments.

A single roll of an 8 can change your game. And the probability of rolling an 8 using the basic version is...

Nada. Zero.

So overall, it may not make much of a difference. But one time, one critical time, it might.